Функция random и процедура randomize
Функция random генерирует случайное вещественное число из промежутка

Возникает естественный вопрос, а как выработать случайное вещественное число из произвольного промежутка [a; b]?
Для этого надо умножить случайное число из промежутка [0; 1], т.е. значение функции random, разность b - a и прибавить левую границу промежутка - a.
Случайное вещественное число из промежутка [a; b] получается от умножения значения функции random на разность b-a и прибавления к результату левой границы промежутка - числа a: random*(b - a) + a
Например, для получения случайного вещественного числа из промежутка

а для получения случайного вещественного числа из промежутка [0; 100] надо значение random умножить на 100: random*100.
Функция random(x), где x - целое число (тип: integer), выдает случайное целое число из промежутка [0; x). Значения функции random(x) имеют тип integer.
Например, значением функции random(6) является случайное целое число из промежутка [0; 6) или из [0; 5].
Как с помощью этой функции получить случайное целое число из промежутка [a; b], где a и b целые числа? Это можно сделать с помощью функции:

Например, случайное целое число из промежутка [15; 18] задается функцией:
random(4)+15.
Есть одна особенность в использовании функций случайных чисел или, как еще их называют, генераторов случайных чисел. При повторном обращении к ним, они могут повторять предыдущие значения. Чтобы избежать этого неприятного явления, перед их применением надо использовать процедуру инициализации этого генератора случайных чисел. Такая процедура есть. Ее имя randomize.
Процедура randomize инициализирует датчик случайных чисел random.
Итак, перед использованием в программе датчика псевдослучайных чисел random в программу надо включать процедуру randomize, которая инициализирует датчик случайных чисел.
Пример 1.
На стержне AB, длина которого равна 36 см, нанесена наудачу тонкая риска. Какова вероятность того, что эта риска окажется не далее a от конца A или не далее b от середины стержня: 1) a = 6 см, b = 2 см; 2) a = 12 см, b = 10 см?
Алгоритм
Числовую ось OX расположим так, что ее начало совпадает с левым концом отрезка - точкой A. Тогда нанесение риски на стержень будет означать случайный выбор значения X из промежутка [0; 36] и задаваться следующим равенством:
x := random*36.
Риска должна быть не далее a от начала отрезка, т. е. значения x должно удовлетворять неравенству (см. рис. 30):

Не далее b от середины отрезка означает, что

Надо подсчитать количество значений x, удовлетворяющих неравенствам:

Пусть их число равно m, а общее число "брошенных" на отрезок точек - n. Тогда искомая вероятность будет равна: p = m/n.
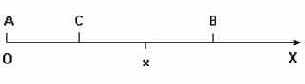
Рис. 30
Для определения точности вычисления вероятности, которая равна частости появления события (m/k), а отсюда и числа испытаний, можно воспользоваться способом, который уже применялся при изучении интегральной формулы Муавра-Лапласа.
В зависимости от гарантированной вероятности и точности вычисления можно установить необходимое число испытаний - n, а затем, по числу испытаний рассчитать вероятность.
Возможность применения формулы Муавра-Лапласа к решению геометрической задачи методом Монте-Карло дает следующие обстоятельства.
Испытания, т.е. "бросание" точек, независимы и равновозможны. Вероятность наступления события в каждом испытании постоянна и отлична от нуля и единицы, а число испытаний может быть достаточно велико.
Таким образом, все условия для применения формулы Муавра-Лапласа выполнены. А теперь вспомним пример, в котором находится число испытаний в зависимости от заданной вероятности и точности вычисления.
Для этого можно использовать процедуры и функции из раздела "Интегральная формула Муавра-Лапласа" (в частности, в примере 6).
Вероятность некоторого события хотят установить статистически.
Для этого проводят некоторое количество испытаний, и частость появления события принимают за его вероятность. Сколько надо произвести испытаний, чтобы с вероятностью 0.97 можно гарантировать, что вероятность события в одном испытании будет отличаться от частости полученной из опыта, не более, чем на 0.01?
Одна из идей, которыми можно воспользоваться и реализовать программными средствами, состоит в том, чтобы непосредственным подбором числа n найти его искомое значение.
Для этого достаточно организовать цикл, завершающим условием которого является:


Чтобы найти x нужно воспользоваться соотношением: x := 2*e*sqrt(n).
В результате можно составить следующую процедуру:
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure
NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1;
x := 2*e*sqrt(n)
until
FF(x) >= PP
end;
Основываясь на этой процедуре составим программу.
{ Применение интегральной формулы Муавра-Лапласа }
Program Problem6;
uses WinCrt;
var
n : longint;
e, pp : real;
{-------------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function
FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{-------------------------------------------------------------------------------------------}
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure
NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1;
x := 2*e*sqrt(n)
until FF(x) >= PP
end;
{-------------------------------------------------------------------------------------------}
{ Основная программа }
begin
write('Введите гарантированную вероятность '); readln(PP);
write('Введите точность вычисления частости '); readln(e);
NumberExperiment(e, PP, n);
writeln('Число испытаний равно ', n );
writeln('С точностью до ', e:1:8)
end.
Используя процедуры из предыдущей программы, составим программу решения геометрической задачи. Надо сразу заметить, что точность вычисления будет невысокой. При увеличении точности даже с гарантированной вероятностью 0.97, не говоря уже о вероятности 0.99, резко возрастает число испытаний и программа становится трудоемкой для выполнения.
Программа
Program Problem1;
uses WinCrt;
var
x, a, b, p, e, pp : real;
i, n, m : longint;
{----------------------------------------------------------------------------------------}
{ Интегральная функция Муавра-Лапласа }
Function FF(x : real) : real;
var
n : integer;
u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u;
n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure
NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1;
x := 2*e*sqrt(n)
until FF(x) >= PP
end;
{----------------------------------------------------------------------------------------}
begin
randomize;
write('Введите расстояние a от конца стержня '); readln(a);
write('Введите расстояние b от середины стержня '); readln(b);
write('Введите гарантированную вероятность '); readln(PP);
write('Введите точность вычисления '); readln(e);
NumberExperiment(e, PP, n);
m := 0;
for i := 1 to n do
begin
x := random*36;
if (x <= a) or (abs(18 - x) <= b) then m := m + 1;
end;
p := m/n;
writeln('Вероятн. появления риски в заданном месте ',p:6:4);
writeln('С точностью до ', e:1:6);
writeln('С гарантированной вероятностью ', PP:1:4);
writeln('При числе испытаний ', n)
end.
Пример 2. На отрезке AB длины l независимо друг от друга выбираются наудачу две точки M и N. Какова вероятность того, что точка M окажется ближе к точке A, чем точка N?
Алгоритм
Пусть |AM| = x, |AN| = y. Рассматриваемому событию будут благоприятствовать лишь те точки, которые удовлетворяют условию y>x. Множество всех возможных исходов испытания можно изобразить в виде квадрата, сторона которого равна l (см. рис. 31).
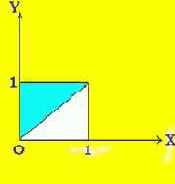
Рис. 31
Множество исходов испытания, благоприятствующих рассматриваемому событию, геометрически изображается точками заштрихованного треугольника.
Координаты всех точек этого треугольника удовлетворяют неравенству: y>x.
Программа
Program Problem2;
uses WinCrt;
var
x, y, p, e, pp : real;
i, n, m : longint;
{--------------------------------------------------------------------------------------}
{ Рекуррентная функция вычисления интеграла вероятностей }
{ Пределы интегрирования от 0 до x. Функция Муавра-Лапласа }
Function
FF(x : real) : real;
var
n : integer; u, I : real;
begin
if x >= 5
then FF := 1
else if x <= -5
then FF := -1
else
begin
u := x; n := 0; I := 0;
repeat
I := I + u; n := n + 1;
u := -u*(x*x*(2*n - 1)/(2*n*(2*n + 1)))
until abs(u) < 0.00001;
FF := 2*I/sqrt(2*Pi)
end
end;
{----------------------------------------------------------------------------------------}
{ Процедура вычисления числа испытаний при заданной гарантиро- }
{ ванной вероятности и заданной точности частости }
Procedure
NumberExperiment(e, PP : real; var n : longint);
var
x : real;
begin
n := 0;
repeat
n := n + 1;
x := 2*e*sqrt(n)
until FF(x) >= PP
end;
{----------------------------------------------------------------------------------------}
begin
randomize;
write('Введите гарантированную вероятность '); readln(PP);
write('Введите точность вычисления '); readln(e);
NumberExperiment(e, PP, n);
m := 0;
for i := 1 to n do
begin
x := random;
y := random;
if y > x then m := m + 1
end;
p := m/n;
writeln('Искомая вероятность равна ', p:6:4);
writeln('С точностью до ', e:1:6);
writeln('С гарантированной вероятностью ', PP:1:4);
writeln('При числе испытаний ', n)
end.
